本学学生が冬の LA シンポジウム 2023 においてLA/EATCS-Japan 学生発表論文賞を受賞しました。
トピックス
掲載日:2024年03月01日
最終更新日:2024年06月13日
2024年2月19日(月)~2月21日(水)の4日間、 京都大学の益川ホールで開催された冬の LA シンポジウム 2023において、大学院情報工学府 情報工学専攻 博士後期課程1年の塩田拓海さんがLA/EATCS-Japan 学生発表論文賞 (LA/EATCS-Japan Student Presentation Award) を受賞しました。
LAシンポジウムは、理論計算機科学の研究者がこの分野のテーマについて自由な議論をするための組織で、1970年から毎年夏と冬にシンポジウムを開き、そのシンポジウムを中心に活動しています。また、本賞は、学生発表者のうちで最優秀の発表者を表彰するものです。
立方体の展開図は11種類あることはよく知られた事実で、いずれの展開図も重なりを持たずに平面上に描くことができます。しかし、多面体およびその切り開き方によって、展開図は重なりを持つことが知られており、平面に描くことができません。
本研究は回転展開と呼ばれる重なりを持つ展開図の発見技法と ZDD と呼ばれる列挙技法を組み合わせることにより、整面凸多面体に属する多面体における重なりを持たない辺展開図を数え上げることに成功しました。例えば、整面凸多面体の一つである切頂十二面体においては、4,982,259,375,000,000,000個の辺展開図に対し、重なりを持たないものの数は 931,603,573,888,462,350個(全体のうち約18.6%)で、大半の辺展開図が重なりを持つことが判明しました。
なお、本研究は、塩田 拓海さん(九州工業大学)、榎本 優大さん、 堀山 貴史教授(北海道大学)、斎藤 寿樹准教授(九州工業大学)の4名による共同研究です。
受賞対象
受賞者:
論文題目:
指導教員:
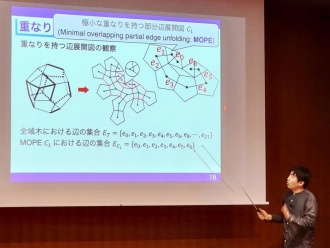
塩田さんによる講演時の写真

(左)北海道大学の堀山貴史教授、(右)塩田拓海さん

賞状